Linear Algebra

Let A be an mx n matrix. The space spanned by the rows of A is called the row space of A, denoted RS(A); it is a subspace of R n. The space spanned by the columns of A is called the column space of A, denoted CS(A); it is a subspace of R m. Rally { r first, r 2,…, r m} consisting of rows of A may not form the basis for RS(A), since the set may not be linearly independent. However, a maximal linearly independent subset of { r first, r 2,…, r m} provides the basis for the store space. Since the maximum number of linearly independent rows of A is equal to the term of A, Read: how to find the row space Similarly, if c first, c 2,…, c n represents the columns of A, then a maximal linearly independent subset of { c first, c 2,…, c n} is the basis for the column space A. 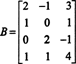But the maximum number of linearly independent columns is also equal to the rank of the matrix, so Therefore, even though RS(A) is a subspace of CHEAP n and CS(A) is a subspace of CHEAP m, equation Linear Algebra 3even if m ≠ n.example 1 Linear Algebra 4 Linear Algebra 5 Linear Algebra 6 Linear Algebra 7 Read more: Scissor Care and Organization Ideas Note that since the store space is a 3-dimensional subspace of CHEAP 3, it must be all CHEAP3.Criteria for membership in column space . If A is a matrix mxn and x is a vector n-, written as a column matrix, then the product A xLinear Algebra 8 By definition, a vector b In CHEAP m is in the column space of A if it can be written as a linear combination of the columns of A. 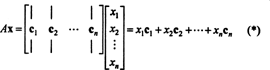That is, b Linear Algebra 9 20319Linear Algebra 10 Example 2 : For what value of b is the vector 20320 [ A/ b] Linear Algebra 11 20321 [ A′/ b′]Linear Algebra 12 Since the bottom zero row of A (short form of A), the bottom entry in the last column must also be 0 — creating a complete row of trailing zeros —To place an order for the A system x = 20322 13 . Linear Algebra So, [ A/ b] b [ A′/ b′]= (1, 2, 3, b) T is in CS(A) if and only if b = 5 Since the basic row operations do not change the rank of the matrix, it is obvious that in the above calculation, the A grade = A rating and rating [ A′/ b′] = rating [ A′/ b′] . (Since the bottom row of A ′ consists entirely of zeros, the rating A ′ = 3, implies also the rating A = 3.) For b = 5, the bottom row of [ A′/ b′] also completely composed of zeros, rank [ A′/ b′] = 3. However, if b is not equal to 5, then the bottom row of will not completely include zeros and ratings of would have been 4, not 3. 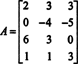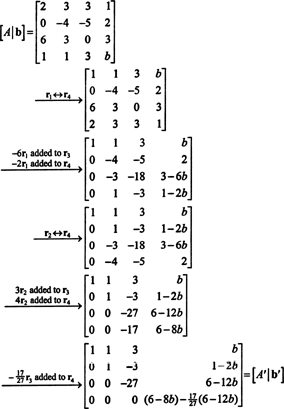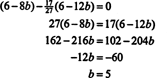This example illustrates the following general fact: When [ A/ b] b is in CS(A), the rank of same class of A; and vice versa, when [ A/ b] b 20323Linear Algebra 14 20324 Linear Algebra 15 from Example 1 above Because the size of a matrix’s column space is always equal to the size of its row space, CS(B) must also have dimension 3: CS(B) is a 3-dimensional subspace of the CHEAP 2032516 . 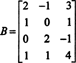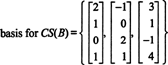Linear Algebra 20326 17 . 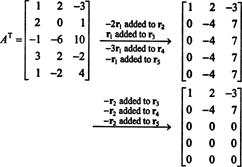Linear Algebra Since the column space of A includes exactly those vectors b such that A x = b being a solvable system, one way to determine the basis for CS(A) would be to first find the space of all vectors b such that A x =2032720328 Linear Algebra 19 Furthermore, since { v first,20329 Linear Algebra 20 is the basis for CS(A), the 2-dimensional subspace of R 3.Read more: how long does it take to build a deck of cards | Top Q&A