How To Identify The Claim In Hypothesis Testing?

Section 1The previous two chapters introduced methods for organizing and summarizing sample data, and using sample statistics to estimate population parameters. This chapter introduces the next major topic of inferential statistics: hypothesis testing.A hypothesis is a statement or claim about a property of a population.Reading: how to identify the claim in hypothesis testing?

The Fundamentals of Hypothesis Testing

When conducting scientific research, typically there is some known information, perhaps from some past work or from a long accepted idea. We want to test whether this claim is believable. This is the basic idea behind a hypothesis test:

• State what we think is true.
• Quantify how confident we are about our claim.
• Use sample statistics to make inferences about population parameters.

For example, past research tells us that the average life span for a hummingbird is about four years. You have been studying the hummingbirds in the southeastern United States and find a sample mean lifespan of 4.8 years. Should you reject the known or accepted information in favor of your results? How confident are you in your estimate? At what point would you say that there is enough evidence to reject the known information and support your alternative claim? How far from the known mean of four years can the sample mean be before we reject the idea that the average lifespan of a hummingbird is four years?Hypothesis testing is a procedure, based on sample evidence and probability, used to test claims regarding a characteristic of a population.A hypothesis is a claim or statement about a characteristic of a population of interest to us. A hypothesis test is a way for us to use our sample statistics to test a specific claim.

Components of a Formal Hypothesis Test

The null hypothesis is a statement about the value of a population parameter, such as the population mean (µ) or the population proportion (p). It contains the condition of equality and is denoted as H0 (H-naught).H0 : µ = 157 or H0 : p = 0.37The alternative hypothesis is the claim to be tested, the opposite of the null hypothesis. It contains the value of the parameter that we consider plausible and is denoted as H1 .H1 : µ > 157 or H1 : p ≠ 0.37The test statistic is a value computed from the sample data that is used in making a decision about the rejection of the null hypothesis. The test statistic converts the sample mean (x̄) or sample proportion (p̂) to a Z- or t-score under the assumption that the null hypothesis is true. It is used to decide whether the difference between the sample statistic and the hypothesized claim is significant.The p-value is the area under the curve to the left or right of the test statistic. It is compared to the level of significance (α).The critical value is the value that defines the rejection zone (the test statistic values that would lead to rejection of the null hypothesis). It is defined by the level of significance.The level of significance (α) is the probability that the test statistic will fall into the critical region when the null hypothesis is true. This level is set by the researcher.The conclusion is the final decision of the hypothesis test. The conclusion must always be clearly stated, communicating the decision based on the components of the test. It is important to realize that we never prove or accept the null hypothesis. We are merely saying that the sample evidence is not strong enough to warrant the rejection of the null hypothesis. The conclusion is made up of two parts:1) Reject or fail to reject the null hypothesis, and 2) there is or is not enough evidence to support the alternative claim.Option 1) Reject the null hypothesis (H0). This means that you have enough statistical evidence to support the alternative claim (H1).Option 2) Fail to reject the null hypothesis (H0). This means that you do NOT have enough evidence to support the alternative claim (H1).Another way to think about hypothesis testing is to compare it to the US justice system. A defendant is innocent until proven guilty (Null hypothesis—innocent). The prosecuting attorney tries to prove that the defendant is guilty (Alternative hypothesis—guilty). There are two possible conclusions that the jury can reach. First, the defendant is guilty (Reject the null hypothesis). Second, the defendant is not guilty (Fail to reject the null hypothesis). This is NOT the same thing as saying the defendant is innocent! In the first case, the prosecutor had enough evidence to reject the null hypothesis (innocent) and support the alternative claim (guilty). In the second case, the prosecutor did NOT have enough evidence to reject the null hypothesis (innocent) and support the alternative claim of guilty.

The Null and Alternative Hypotheses

There are three different pairs of null and alternative hypotheses:where c is some known value.

A Two-sided Test

This tests whether the population parameter is equal to, versus not equal to, some specific value.Ho: μ = 12 vs. H1: μ ≠ 12The critical region is divided equally into the two tails and the critical values are ± values that define the rejection zones.

A Right-sided Test

This tests whether the population parameter is equal to, versus greater than, some specific value.Ho: μ = 12 vs. H1: μ > 12The critical region is in the right tail and the critical value is a positive value that defines the rejection zone.

A Left-sided Test

This tests whether the population parameter is equal to, versus less than, some specific value.Ho: μ = 12 vs. H1: μ < 12The critical region is in the left tail and the critical value is a negative value that defines the rejection zone.

Statistically Significant

When the observed results (the sample statistics) are unlikely (a low probability) under the assumption that the null hypothesis is true, we say that the result is statistically significant, and we reject the null hypothesis. This result depends on the level of significance, the sample statistic, sample size, and whether it is a one- or two-sided alternative hypothesis.

Types of Errors

When testing, we arrive at a conclusion of rejecting the null hypothesis or failing to reject the null hypothesis. Such conclusions are sometimes correct and sometimes incorrect (even when we have followed all the correct procedures). We use incomplete sample data to reach a conclusion and there is always the possibility of reaching the wrong conclusion. There are four possible conclusions to reach from hypothesis testing. Of the four possible outcomes, two are correct and two are NOT correct.A Type I error is when we reject the null hypothesis when it is true. The symbol α (alpha) is used to represent Type I errors. This is the same alpha we use as the level of significance. By setting alpha as low as reasonably possible, we try to control the Type I error through the level of significance.A Type II error is when we fail to reject the null hypothesis when it is false. The symbol β (beta) is used to represent Type II errors.In general, Type I errors are considered more serious. One step in the hypothesis test procedure involves selecting the significance level (α), which is the probability of rejecting the null hypothesis when it is correct. So the researcher can select the level of significance that minimizes Type I errors. However, there is a mathematical relationship between α, β, and n (sample size).

• As α increases, β decreases
• As α decreases, β increases
• As sample size increases (n), both α and β decrease

The natural inclination is to select the smallest possible value for α, thinking to minimize the possibility of causing a Type I error. Unfortunately, this forces an increase in Type II errors. By making the rejection zone too small, you may fail to reject the null hypothesis, when, in fact, it is false. Typically, we select the best sample size and level of significance, automatically setting β.

Power of the Test

A Type II error (β) is the probability of failing to reject a false null hypothesis. It follows that 1-β is the probability of rejecting a false null hypothesis. This probability is identified as the power of the test, and is often used to gauge the test’s effectiveness in recognizing that a null hypothesis is false.The probability that at a fixed level α significance test will reject H0, when a particular alternative value of the parameter is true is called the power of the test.Power is also directly linked to sample size. For example, suppose the null hypothesis is that the mean fish weight is 8.7 lb. Given sample data, a level of significance of 5%, and an alternative weight of 9.2 lb., we can compute the power of the test to reject μ = 8.7 lb. If we have a small sample size, the power will be low. However, increasing the sample size will increase the power of the test. Increasing the level of significance will also increase power. A 5% test of significance will have a greater chance of rejecting the null hypothesis than a 1% test because the strength of evidence required for the rejection is less. Decreasing the standard deviation has the same effect as increasing the sample size: there is more information about μ. Section 2

Hypothesis Test about the Population Mean (μ) when the Population Standard Deviation (σ) is Known

We are going to examine two equivalent ways to perform a hypothesis test: the classical approach and the p-value approach. The classical approach is based on standard deviations. This method compares the test statistic (Z-score) to a critical value (Z-score) from the standard normal table. If the test statistic falls in the rejection zone, you reject the null hypothesis. The p-value approach is based on area under the normal curve. This method compares the area associated with the test statistic to alpha (α), the level of significance (which is also area under the normal curve). If the p-value is less than alpha, you would reject the null hypothesis.As a past student poetically said: If the p-value is a wee value, Reject HoBoth methods must have:

• Data from a random sample.
• Verification of the assumption of normality.
• A null and alternative hypothesis.
• A criterion that determines if we reject or fail to reject the null hypothesis.
• A conclusion that answers the question.

There are four steps required for a hypothesis test:

State the null and alternative hypotheses.

State the level of significance and the critical value.

Compute the test statistic.

State a conclusion.

The Classical Method for Testing a Claim about the Population Mean (μ) when the Population Standard Deviation (σ) is Known

Testing a Hypothesis using P-values

The p-value is the probability of observing our sample mean given that the null hypothesis is true. It is the area under the curve to the left or right of the test statistic. If the probability of observing such a sample mean is very small (less than the level of significance), we would reject the null hypothesis. Computations for the p-value depend on whether it is a one- or two-sided test.Read more: How to make hair fibers stickSteps for a hypothesis test using p-values:

• State the null and alternative hypotheses.
• State the level of significance.
• Compute the test statistic and find the area associated with it (this is the p-value).
• Compare the p-value to alpha (α) and state a conclusion.

Instead of comparing Z-score test statistic to Z-score critical value, as in the classical method, we compare area of the test statistic to area of the level of significance.The Decision Rule: If the p-value is less than alpha, we reject the null hypothesis

Computing P-values

If it is a two-sided test (the alternative claim is ≠), the p-value is equal to two times the probability of the absolute value of the test statistic. If the test is a left-sided test (the alternative claim is “<”), then the p-value is equal to the area to the left of the test statistic. If the test is a right-sided test (the alternative claim is “>”), then the p-value is equal to the area to the right of the test statistic.Let’s look at Example 6 again.A forester studying diameter growth of red pine believes that the mean diameter growth will be different from the known mean growth of 1.35 in./year if a fertilization treatment is applied to the stand. He conducts his experiment, collects data from a sample of 32 plots, and gets a sample mean diameter growth of 1.6 in./year. The population standard deviation for this stand is known to be 0.46 in./year. Does he have enough evidence to support his claim?Step 1) State the null and alternative hypotheses.

• Ho: μ = 1.35 in./year
• H1: μ ≠ 1.35 in./year

Step 2) State the level of significance.

• We will choose a level of significance of 5% (α = 0.05).

Step 3) Compute the test statistic.

• For this problem, the test statistic is:

The p-value is two times the area of the absolute value of the test statistic (because the alternative claim is “not equal”).

• Look up the area for the Z-score 3.07 in the standard normal table. The area (probability) is equal to 1 – 0.9989 = 0.0011.
• Multiply this by 2 to get the p-value = 2 * 0.0011 = 0.0022.

Step 4) Compare the p-value to alpha and state a conclusion.

• Use the Decision Rule (if the p-value is less than α, reject H0).
• In this problem, the p-value (0.0022) is less than alpha (0.05).
• We reject the H0. We have enough evidence to support the claim that the mean diameter growth is different from 1.35 inches/year.

Let’s look at Example 7 again.A researcher believes that there has been an increase in the average farm size in his state since the last study five years ago. The previous study reported a mean size of 450 acres with a population standard deviation (σ) of 167 acres. He samples 45 farms and gets a sample mean of 485.8 acres. Is there enough information to support his claim?Step 1) State the null and alternative hypotheses.

• Ho: μ = 450 acres
• H1: μ >450 acres

Step 2) State the level of significance.

• We will choose a level of significance of 5% (α = 0.05).

Step 3) Compute the test statistic.

• For this problem, the test statistic is

The p-value is the area to the right of the Z-score 1.44 (the hatched area).

• This is equal to 1 – 0.9251 = 0.0749.
• The p-value is 0.0749.

Step 4) Compare the p-value to alpha and state a conclusion.

• Use the Decision Rule.
• In this problem, the p-value (0.0749) is greater than alpha (0.05), so we Fail to Reject the H0.
• The area of the test statistic is greater than the area of alpha (α).

We fail to reject the null hypothesis. We do not have enough evidence to support the claim that the mean farm size has increased.Let’s look at Example 8 again.A researcher believes that there has been a reduction in the mean number of hours that college students spend preparing for final exams. A national study stated that students at a 4-year college spend an average of 23 hours preparing for 5 final exams each semester with a population standard deviation of 7.3 hours. The researcher sampled 227 students and found a sample mean study time of 19.6 hours. Does this indicate that the average study time for final exams has decreased? Use a 1% level of significance to test this claim.Step 1) State the null and alternative hypotheses.

• H0: μ = 23 hours
• H1: μ < 23 hours

Step 2) State the level of significance.

• This is a left-sided test so alpha (0.01) is all in the left tail.

Step 3) Compute the test statistic.

• For this problem, the test statistic is

The p-value is the area to the left of the test statistic (the little black area to the left of -7.02). The Z-score of -7.02 is not on the standard normal table. The smallest probability on the table is 0.0002. We know that the area for the Z-score -7.02 is smaller than this area (probability). Therefore, the p-value is <0.0002.Step 4) Compare the p-value to alpha and state a conclusion.

• Use the Decision Rule.
• In this problem, the p-value (p<0.0002) is less than alpha (0.01), so we Reject the H0.
• The area of the test statistic is much less than the area of alpha (α).

We reject the null hypothesis. We have enough evidence to support the claim that the mean final exam study time has decreased below 23 hours.Both the classical method and p-value method for testing a hypothesis will arrive at the same conclusion. In the classical method, the critical Z-score is the number on the z-axis that defines the level of significance (α). The test statistic converts the sample mean to units of standard deviation (a Z-score). If the test statistic falls in the rejection zone defined by the critical value, we will reject the null hypothesis. In this approach, two Z-scores, which are numbers on the z-axis, are compared. In the p-value approach, the p-value is the area associated with the test statistic. In this method, we compare α (which is also area under the curve) to the p-value. If the p-value is less than α, we reject the null hypothesis. The p-value is the probability of observing such a sample mean when the null hypothesis is true. If the probability is too small (less than the level of significance), then we believe we have enough statistical evidence to reject the null hypothesis and support the alternative claim.

Software Solutions

Minitab

(referring to Ex. 8)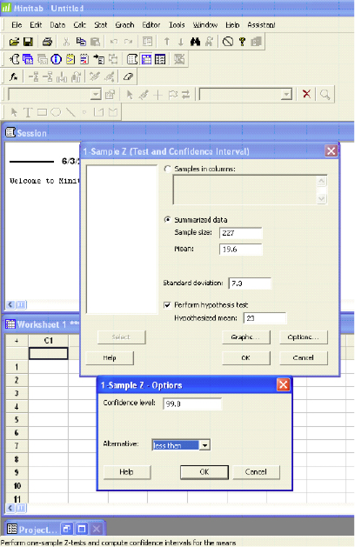One-Sample Z Test of mu = 23 vs. < 23 The assumed standard deviation = 7.3 99% Upper N Mean SE Mean Bound Z P 227 19.600 0334390000 -7.02 0.000

Excel

Excel does not offer 1-sample hypothesis testing. Section 3

Hypothesis Test about the Population Mean (μ) when the Population Standard Deviation (σ) is Unknown

Frequently, the population standard deviation (σ) is not known. We can estimate the population standard deviation (σ) with the sample standard deviation (s). However, the test statistic will no longer follow the standard normal distribution. We must rely on the student’s t-distribution with n-1 degrees of freedom. Because we use the sample standard deviation (s), the test statistic will change from a Z-score to a t-score.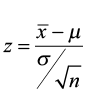 → Steps for a hypothesis test are the same that we covered in Section 2.

• State the null and alternative hypotheses.
• State the level of significance and the critical value.
• Compute the test statistic.
• State a conclusion.

Just as with the hypothesis test from the previous section, the data for this test must be from a random sample and requires either that the population from which the sample was drawn be normal or that the sample size is sufficiently large (n≥30). A t-test is robust, so small departures from normality will not adversely affect the results of the test. That being said, if the sample size is smaller than 30, it is always good to verify the assumption of normality through a normal probability plot.We will still have the same three pairs of null and alternative hypotheses and we can still use either the classical approach or the p-value approach.Selecting the correct critical value from the student’s t-distribution table depends on three factors: the type of test (one-sided or two-sided alternative hypothesis), the sample size, and the level of significance.For a two-sided test (“not equal” alternative hypothesis), the critical value (tα/2), is determined by alpha (α), the level of significance, divided by two, to deal with the possibility that the result could be less than OR greater than the known value.

• If your level of significance was 0.05, you would use the 0.025 column to find the correct critical value (0.05/2 = 0.025).
• If your level of significance was 0.01, you would use the 0.005 column to find the correct critical value (0.01/2 = 0.005).

For a one-sided test (“a less than” or “greater than” alternative hypothesis), the critical value (tα) , is determined by alpha (α), the level of significance, being all in the one side.

• If your level of significance was 0.05, you would use the 0.05 column to find the correct critical value for either a left or right-side question. If you are asking a “less than” (left-sided question, your critical value will be negative. If you are asking a “greater than” (right-sided question), your critical value will be positive.

The level of significance is the probability that you, as the researcher, set to decide if there is enough statistical evidence to support the alternative claim. It should be set before the experiment begins.

P-value Approach

We can also use the p-value approach for a hypothesis test about the mean when the population standard deviation (σ) is unknown. However, when using a student’s t-table, we can only estimate the range of the p-value, not a specific value as when using the standard normal table. The student’s t-table has area (probability) across the top row in the table, with t-scores in the body of the table.

• To find the p-value (the area associated with the test statistic), you would go to the row with the number of degrees of freedom.
• Go across that row until you find the two values that your test statistic is between, then go up those columns to find the estimated range for the p-value.

Conclusion

If your level of significance is 5%, you would reject the null hypothesis as the p-value (0.01-0.02) is less than alpha (α) of 0.05.If your level of significance is 1%, you would fail to reject the null hypothesis as the p-value (0.01-0.02) is greater than alpha (α) of 0.01.Software packages typically output p-values. It is easy to use the Decision Rule to answer your research question by the p-value method.

Software Solutions

Minitab

Read more: how to do laundry in nyc(referring to Ex. 12)One-Sample TTest of mu = 0.5 vs. > 0.595% LowerNMeanStDevSE MeanBoundTP510.59000.29000.04060.52192.220.016

Excel

Excel does not offer 1-sample hypothesis testing. Section 4

Hypothesis Test for a Population Proportion (p)

Frequently, the parameter we are testing is the population proportion.

• We are studying the proportion of trees with cavities for wildlife habitat.
• We need to know if the proportion of people who support green building materials has changed.
• Has the proportion of wolves that died last year in Yellowstone increased from the year before?

Recall that the best point estimate of p, the population proportion, is given bywhere x is the number of individuals in the sample with the characteristic studied and n is the sample size. The sampling distribution of p̂ is approximately normal with a mean 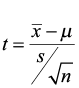and a standard deviationwhen np(1 – p)≥10. We can use both the classical approach and the p-value approach for testing.The steps for a hypothesis test are the same that we covered in Section 2.

• State the null and alternative hypotheses.
• State the level of significance and the critical value.
• Compute the test statistic.
• State a conclusion.

The test statistic follows the standard normal distribution. Notice that the standard error (the denominator) uses p instead of p̂, which was used when constructing a confidence interval about the population proportion. In a hypothesis test, the null hypothesis is assumed to be true, so the known proportion is used.

• The critical value comes from the standard normal table, just as in Section 2. We will still use the same three pairs of null and alternative hypotheses as we used in the previous sections, but the parameter is now p instead of μ:

• For a two-sided test, alpha will be divided by 2 giving a ± Zα/2 critical value.
• For a left-sided test, alpha will be all in the left tail giving a – Zα critical value.
• For a right-sided test, alpha will be all in the right tail giving a Zα critical value.

Software Solutions

Minitab

(referring to Ex. 15)Test and CI for One ProportionTest of p = 0.32 vs. p > 0.3290% Lower Sample X N Sample p Bound Z-Value p-Value 1 79 196 0334390000 8160 2.49 0.006 Using the normal approximation.

Excel

Excel does not offer 1-sample hypothesis testing. Section 5

Hypothesis Test about a Variance

When people think of statistical inference, they usually think of inferences involving population means or proportions. However, the particular population parameter needed to answer an experimenter’s practical questions varies from one situation to another, and sometimes a population’s variability is more important than its mean. Thus, product quality is often defined in terms of low variability.Sample variance S2 can be used for inferences concerning a population variance σ2. For a random sample of n measurements drawn from a normal population with mean μ and variance σ2, the value S2 provides a point estimate for σ2. In addition, the quantity (n – 1)S2 / σ2 follows a Chi-square (χ2) distribution, with df = n – 1.The properties of Chi-square (χ2) distribution are:

• Unlike Z and t distributions, the values in a chi-square distribution are all positive.
• The chi-square distribution is asymmetric, unlike the Z and t distributions.
• There are many chi-square distributions. We obtain a particular one by specifying the degrees of freedom (df = n – 1) associated with the sample variances S2.

One-sample χ2 test for testing the hypotheses:Null hypothesis: H0: σ2 = 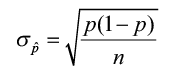(constant)Alternative hypothesis:where the χ2 critical value in the rejection region is based on degrees of freedom df = n – 1 and a specified significance level of α.Test statistic: .As with previous sections, if the test statistic falls in the rejection zone set by the critical value, you will reject the null hypothesis.

Software Solutions

Minitab

(referring to Ex. 16)Test and CI for One VarianceMethod Null hypothesis Sigma-squared = 0.06 Alternative hypothesis Sigma-squared > 0.06The chi-square method is only for the normal distribution.TestsTest Method Statistic DF P-Value Chi-Square 10.67 10 0.384

Excel

Excel does not offer 1-sample χ2 testing.Read more: How to uninstall faceit from computer Section 6

Putting it all Together Using the Classical Method

To Test a Claim about μ when σ is Known

• Write the null and alternative hypotheses.
• State the level of significance and get the critical value from the standard normal table.
• Compute the test statistic.

• Compare the test statistic to the critical value (Z-score) and write the conclusion.

To Test a Claim about μ When σ is Unknown

• Write the null and alternative hypotheses.
• State the level of significance and get the critical value from the student’s t-table with n-1 degrees of freedom.
• Compute the test statistic.

• Compare the test statistic to the critical value (t-score) and write the conclusion.

To Test a Claim about p

• Write the null and alternative hypotheses.
• State the level of significance and get the critical value from the standard normal distribution.
• Compute the test statistic.

• Compare the test statistic to the critical value (Z-score) and write the conclusion.

To Test a Claim about Variance

• Write the null and alternative hypotheses.
• State the level of significance and get the critical value from the chi-square table using n-1 degrees of freedom.
• Compute the test statistic.

• Compare the test statistic to the critical value and write the conclusion.

Last, Wallx.net sent you details about the topic “How To Identify The Claim In Hypothesis Testing?❤️️”.Hope with useful information that the article “How To Identify The Claim In Hypothesis Testing?” It will help readers to be more interested in “How To Identify The Claim In Hypothesis Testing? [ ❤️️❤️️ ]”.

Posts “How To Identify The Claim In Hypothesis Testing?” posted by on 2021-10-23 13:26:07. Thank you for reading the article at wallx.net