How To Find The Reciprocal Of A Negative Number
Video How to find the inverse of a number Negative reciprocal – Explanation and examples Negative reciprocity sounds complicated, but once we understand its concept, you will see the application and finding of negative reciprocity of some how easy. Why don’t we dissect these two words?Negative and inverse – this means that the negative inverse of a number is the result of multiplying the inverse of the number by $mathbf {-1} $. Read: how to find the reciprocal of a negative number Simply put as its definition, negative inverse has many applications including finding perpendicular slopes and modeling real world applications using inverse relationships.
What is negative reciprocity?
When dealing with negative reciprocity numbers, we will first recall what these two words stand for in math: negative and reciprocal. $ Boldsymbol {dfrac {a} {b} rightarrow – dfrac {b} {a}} $ We will slowly analyze this form, and by the end of this article you will certainly be able to understand what this represents. for what.ReciprocalThe inverse of a number or a function is the value or expression that results from reversing the positions of the numerator and denominator. $boldsymbol {dfrac {a} {b} rightarrow dfrac {b} {a}} $ The reciprocals are considered as multiplication reciprocals because they will always be 1 when we multiply a number by its reciprocal. $ dfrac {a} {b} cdot dfrac {b} {a} = 1 $ Master your knowledge of inverse numbers here.Negation of a number (or a function)The negative of a number or a function is the result of a number multiplied by -1. Let’s say we have a fraction, $dfrac{b}{a}$, its opposite would be $-dfrac{b}{a}$. $ Boldsymbol {-1 cdot dfrac {b} {a} = -dfrac { b} {a}} $ Learn more about negative numbers here. When we combine these two concepts, we get the negative inverse of a number. This means that negative inverses are the result of us taking the inverse of a number then finding the negative value of the result. Thus we have $boldsymbol {dfrac {a} {b} rightarrow – dfrac {b} {a}} $.
How to find negative reciprocal?
Now that we understand what negative reciprocity stands for, how do we manipulate the different forms of expressions to get their negative reciprocals?
- Always start by convert position of numerator and denominator of fractions.
- When we have reciprocity, multiply the result by $mathbf {-1} $.
We’ve created quick guides that you can keep in mind when working with different types of numbers and expressions. Let’s start by learning how to find negative inverse of a fraction$ dfrac {a} {b} $, where $ b neq 0 $.What if we are working with rational functions like $dfrac{p(x)}{q(x)}$? We apply the same process as we did with fractions.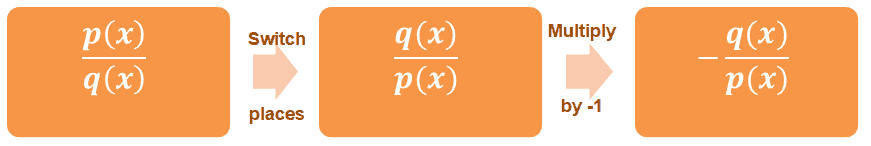
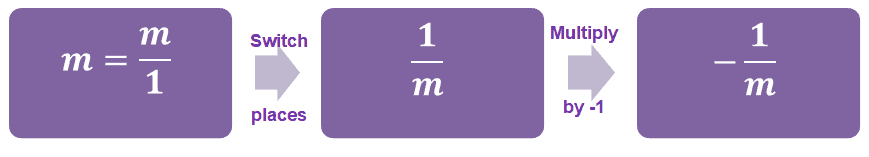
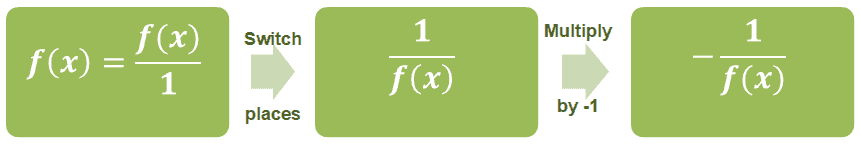
The rational function and its negative inverse will be valid only when $p(x) neq 0 $ and $ q (x) neq 0 $. we are working with integers afterward? we start by expressing the whole number as a fraction with $1 as its denominator. Assuming we have $m as an integer, we start by expressing it as dfrac{m}{1}$ and follow the same process.
The same procedure applies to functions like $f(x)$ unreasonable functionRead more: 20 Homemade snow plows – How to build a snow plow
Note that for opposites to exist, neither $m$ nor $f(x)$ must equal $0. First, let’s go ahead and summarize what we’ve learned so far about negative reciprocals.
Summary of definitions and reciprocal properties
- This expression represents what happens when finding counterpoint numbers: $ boldsymbol {dfrac {a} {b} rightarrow – dfrac {b} {a}} $.
- When given an integer or a non-rational function, start by expressing the given number as the fraction 1.
- It is only possible for a constant or a function to have a negative inverse when both its numerator and denominator are not equal to $0.
- Slope of a perpendicular using negative inverse.
That’s it. Remember to keep these notes in mind when dealing with the issues below.example 1Complete the table below by finding the corresponding negative inverses of the following values.First valueNegative reciprocal$ dfrac {1} {2} $ $ -dfrac {2} {3} $ 9 $ $ – 4dfrac {1} {7} $ Solution When finding the opposite number, we start by shifting the numerator position number and denominator of the fraction. Let’s work with the first two items first: $dfrac{1}{2}$ and $-dfrac{2}{3}$. Therefore, their reciprocals are $dfrac{2}{1}$ and $-dfrac{3}{2}$. For each value, multiply by $-1 $ to find the corresponding negative inverse.
- $ -1 cdot dfrac {2} {1} = -2 $
- $ -1 cdot -dfrac {3} {2} = dfrac {3} {2} $.
We’ll actually apply the same process to the last two rows, but make sure we rewrite them as fractions first. The whole number $9 can be written as $dfrac{9}{1}$ and the mixed number $- 4dfrac{1}{7}$ can be written as $-dfrac{29}{7}$. After we have them in fraction form, we can now swap the positions of the numerators and their respective denominators, and then multiply the corresponding result by -1$.
- $ begin {align} dfrac {9} {1} rightarrow dfrac {1} {9} rightarrow -dfrac {1} {9} end {align} $
- $ begin {align} -dfrac {29} {7} rightarrow dfrac {-7} {29} rightarrow dfrac {7} {29} end {align} $
Thus, we have the complete table as shown below.First valueNegative reciprocal$ dfrac {1} {2} $$ – 2 $$ – dfrac {2} {3} $$ dfrac {3} {2} $$9 $$ – dfrac {1} {9} $$ – 4dfrac {1 } {7} $$ – dfrac {7} {29} $Example 2Call $h(x)$ the inverse of $f(x)$ for each of the following functions. Find $h(x)$. What are the restrictions on $x$ in each case? A. $f(x) = dfrac {1} {x – 1} $b. $f(x) = dfrac {2} {3 (x +2)} $c. $ f(x) = x ^ 2 – 3x – 54 $ Solution We apply the same procedure when finding negative inverses of functions. a. This means we start by converting the positions of $1 and $x – 1 to find the inverse of $f(x)$. Then we multiply the result by $-1$. $ Begin {align} h(x) &= – 1cdot dfrac {x-1} {1} &= – 1cdot x – 1 & mathbf {-x + 1} end {align} $ Because $h(x) $ is a linear expression so it has no restrictions. However, the function $f(x)$ must not have $x – 1 = 0$, so $mathbf{x neq 0}$. B. We apply the same procedure from a. Hence, we have $h(x)$ as shown below. $ Begin {align} h(x) & = – 1cdot dfrac {3 (x + 2)} {2} & = – 1cdot dfrac {3x + 6} {2} & = mathbf {-dfrac {3x + 6 } {2}} end {align} $ The function $h(x)$ has a constant as its denominator, so it has no limit on $x$. However, the function f(x)$ cannot have 3(x + 2) = 0$, so $mathbf{x neq -2}$. C. Express f(x)$ as a fraction by having $1 as its denominator, so f(x) = dfrac{x^2 – 3x – 54}{1}$. Now, apply the same procedure to find the number of opposites, $h(x)$. $ Begin {align} h(x) & = – 1cdot dfrac {1} {x ^ 2-3x-54} & = mathbf { -dfrac {1} {x ^ 2-3x-54}} end { align } $ Since $f(x)$ is a polynomial, it has no limit on $x$. However, its negative inverse cannot have a zero in its denominator. We can find the restrictions for $h(x)$ by finding the values where $x^2 – 3x – 54$ is 0.Read more: How to change the rear tire on a lawn mower for cadet $ begin {align} x ^ 2 -3x – 54 & = 0 (x – 9) (x + 6) & = 0 x & = 9 x & -6end {align} $ This means is for $h(x)$ to be valid, $mathbf{x neq{-6.9}}$.Example 3The graph of the linear function, f(x)$, perpendicular to the graph of h(x)$, is also a linear function. If f(x)$ has a slope of $ -dfrac{2}{3}$, what is the slope of h(x)$? slopes of perpendiculars Since we have the slope f(x)$, we can find the slope of h(x)$ by finding the inverse of $ -dfrac {2} {3} $. $ begin { align } m_perp & = -1 cdot-dfrac {3} {2} & = dfrac {3} {2} end {align} $ This means the slope of $h(x)$ is $dfrac{3}{2}$ so that it is perpendicular to $f(x)$.Example 4The inverse of $f(x)$ is $dfrac{x^2 – 2}{x – 5}$. What is the expression for $f(x)$? Solution This time, we introduce the negative inverse. We need to find the expression for $f(x)$ by reversing the steps:
- We start by multiplying -1$ back by the negative inverse to reverse the changes in sign.
- Swap the positions of the negative reciprocal numerator and denominator.
$ begin {align} f(x) &= – 1cdot dfrac {x-5} {x^2-2} &= dfrac {-x + 5} {x^2-2} end {align} $This means $mathbf{f(x)=dfrac{-x+5}{x^2-2}}$. What about the steps? They are actually the same process because The negative inverse of the negative inverse of a function would be $mathbf{f(x)} $.Example 6If a given number is twenty-seven times greater than the square of its negative inverse, find the number. Solution Let $n $ be the number we are looking for, so its negative number can be expressed as $ -dfrac {1} {n} $ . Set up the equation representing the situation. $ N = 27cdotleft (-dfrac {1} {n} right) ^ 2 $ Simplify this equation by multiplying both sides of the equation by $ n ^ 2 $ and taking the square root of both sides of the equation submit. $ begin { align } n & = dfrac { 27 } { n ^ 2 } n ^ 3 & = 27 sqrt[3]{n^3} & = sqrt[3]{27} n &= 3 end {align} $ This means that for the number satisfying the condition, it should be 3.Practice questions1. Complete the table below by finding the corresponding negative inverses of the following values.First valueNegative reciprocal$dfrac{1}{5}$$-dfrac{6}{11}$$-12$$2dfrac{3}{8}$2. Let $h(x)$ be the inverse of $f(x) $ for each of the following functions. Find $h(x)$. What are the restrictions on $x$ in each case? A. $f(x) = dfrac {2} {3x – 5} $b. $f(x) = dfrac {x} {2 (x – 3)} $c. $f(x) = x^2 – 7x – 30$ d. $f(x) = 1 + dfrac {1} {x – 2} $3. True or false? The inverse of the negative variable of a function is equal to the function itself.4. The graph of the linear function, f(x)$, perpendicular to the graph of h(x)$, is also a linear function. If f(x)$ has a slope of -2dfrac{1}{5}$ what is the slope of h(x)$? 5. The reciprocal of $f(x)$ is $dfrac{x^2 – 2}{x – 5}$. What is the expression for $f(x)$? 6. Let $h(x)$ be the inverse of $f(x)$. A. What is the expression for $h(x)$ given that $f(x) = dfrac{4x – 3}{2}$? B. What restrictions on $x$ so that both f(x)$ and h(x)$ exist? C. Use your knowledge to graph the inverse function to graph $h(x)$. Includes vertical and horizontal non-fixed markings. If a given number is sixty-four times greater than the square of its negative inverse, find the number. Read more: How to get off the gangstalking listPrevious Post | Main page | Next lesson
Last, Wallx.net sent you details about the topic “How To Find The Reciprocal Of A Negative Number❤️️”.Hope with useful information that the article “How To Find The Reciprocal Of A Negative Number” It will help readers to be more interested in “How To Find The Reciprocal Of A Negative Number [ ❤️️❤️️ ]”.
Posts “How To Find The Reciprocal Of A Negative Number” posted by on 2021-11-08 10:35:36. Thank you for reading the article at wallx.net
