How To Check If A Vector Field Is Conservative

As mentioned in the context of the gradient theorem, the vector field $dlvf$ is conservative if and only if it has a potential function $f$ with $dlvf = nabla f$. Therefore, if you are given a potential function f$ or if you can find a potential function and that potential function is defined everywhere, then you don’t need to do anything. You know that $dlvf$ is a conservative vector field and you don’t need to worry about the other tests we cover here. Similarly, if you can prove that it is not possible to find a function $f$ satisfying $dlvf = nabla f$, then you can also conclude that $dlvf$ is non-conservative or path-dependent. You can skip this discussion about checking for path dependencies and go straight to the potential function finding procedure. If this works or if it breaks, you found your answer on whether $dlvf$ is conservative. However, if you’re like many of us and are prone to making one or two mistakes in a multi-step process, you might benefit from other tests that can quickly determine path independence. That way you can avoid looking for a potential function when it doesn’t exist and benefit from validation tests of your computation. If $dlvf$ is a three-dimensional vector field, then $dlvf:R^3 to R^3$ (confusion?), then we can infer another condition. This condition is based on the fact that the vector field $dlvf$ is conservative if and only if $dlvf = nabla f$ for some potential function. We can calculate that the curvature of a gradient is zero, $ curl nabla f = vc{0}$, with any two distinct continuums from f:R^3 to R$. Therefore, if $dlvf$ is maintained, its curvature should be zero, because $curl dlvf = curl nabla f = vc{0}$. Read more: how to get rid of weeds naturally without killing st augustine grass -dimensional vector field, $dlvf:R^2 to R^2$, we can similarly conclude that if the vector field is preserve, then the scalar scroll should be zero, $$ pdiff {dlvfc_2} {x} -pdiff {dlvfc_1 } {y} = frac {part f^2} {part x part y} -frac {part f^2} {part y part x} = 0. $$ We have to be careful here. A valid statement is that if $dlvf$ is conservative, its curvature should be zero. If there are no additional conditions on the vector field, the converse might not be true, so we cannot conclude that $dlvf$ is conservative just because its curvature is zero. There are dependent vector fields. path with zero curvature. On the other hand, we can conclude that if the curl of $dlvf$ is non-zero, then $dlvf$ must depend on the path. We can link the previous two tests (tests 2 and 3). Experiment 2 says that the lack of “macro circulation” is sufficient to determine path independence, but the problem is that the lack of circulation around any closed curve is difficult to test directly. Experiment 3 states that the conservative vector field has no “microcircle” as obtained by the curve. It’s easy to check for lack of curvature, but the problem is that lack of curvature is not enough to determine path independence. zero “microcirculation.” This link is exactly what both Green’s theorem and Stokes’ theorem provide. Don’t worry if you haven’t learned both of these theorems. The basic idea is simple enough: the “macrocycle” around a closed curve is equal to the sum of the “microcircles” in the flat region inside the curve (for two dimensions, Green’s theorem) or in a surface whose boundary is a curve (for three dimensions, Stokes theorem). Let’s check the case of a bidirectional vector field with scalar curl $ pdiff {dlvfc_2} {x} -pdiff {dlvfc_1} {y} $ being zero. If we have a closed curve $dlc$ where $dlvf$ is defined everywhere within it, then we can apply Green’s theorem to conclude that the “macro cycle” $dlint $ around $dlc$ is equal to the sum of the “microcircles” inside $dlc$. We can actually conclude that the “macrocycle” is zero from the fact that the “microcircle” $pdiff {dlvfc_2} {x} -pdiff {dlvfc_1} {y} $ is zero everywhere where inside $dlc$.According to test 2, to conclude that $dlvf$ is conservative, we need $dlint$ to be zero around every closing curve $dlc$. If the vector field is defined inside every closed curve $dlc$ and the “microcircle” is zero everywhere inside each curve, then Green’s theorem gives us exactly that condition. We can conclude that $dlint = 0 around every closed curve and that the vector field is conservative. curve. In other words, if the region where $dlvf$ is defined has some holes in it, then we cannot apply Green’s theorem to every closed curve $dlc$. In this case, we cannot be certain that zero “microcircle” means zero “macro cycle” and hence path independence. Such a flaw in the definition domain of $dlvf$ is what causes problems in our collation example of a path-dependent field with zero curvature. if the specified region $dlvf$ is simply connected, i.e. the region has no holes through it. In this case we know $dlvf$ is defined inside every closing curve $dlc$ and nothing difficult can happen. We can summarize our test for the path dependence of two-dimensional vector fields as follows. curl is 0, i.e. $$ pdiff {dlvfc_2} {x} -pdiff {dlvfc_1} {y} = 0, $$ everywhere in $dlr$, then $dlvf$ is conserved in the domain $dlr$. It turns out that the results for the three dimensions are essentially the same. If the vector field $dlvf:R^3 to R^3 is continuous distinguishable in a simply connected domain $dlv in R^3 and its curvature is zero, i.e. $ curl dlvf = vc {0}$, everywhere in $dlv$, then $dlvf$ is unique in the domain $dlv$. One small difference between two and three dimensions is what a simple connected region means. Any hole in the two-dimensional domain is enough to make it not simple to connect. However, in three dimensions, a simply connected domain can have a hole in the center, as long as the hole doesn’t go all the way through the region, as illustrated in this figure.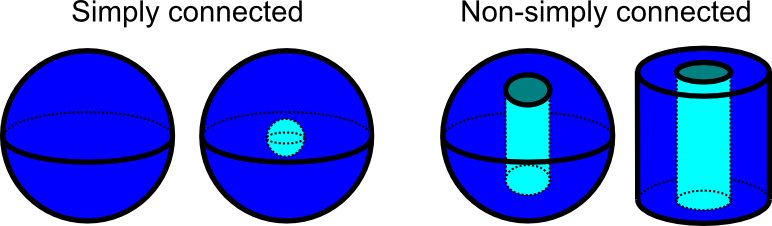The reason a hole in the center of the domain is not a problem in three dimensions is that we have more room to move around in 3D. If we have a non-curved vector field $dlvf$ (i.e. no “microcircle”), we can use Stokes theorem to deduce the absence of a pulsating “macrocycle” around any $dlc$ closing curve. To use Stokes theorem, we only need to find a surface with boundary $dlc$. If the domain $dlvf$ is simply connected, even if it has a flaw that does not go all the way, we can always find such a surface. The surface can only go around any hole in the middle of the domain. With such a surface that $curl dlvf = vc{0}$, we can use Stokes theorem to show that the cycle $dlint$ around $dlc$ is zero. Since we can do this for any closed curve, we can conclude that $dlvf$ is conservative. The flexibility we have in three dimensions to find multiple surfaces with boundaries is a given closed curve illustrated in this applet that we use to introduce Stokes’ Of course, if the $dlv$ region is not simply connected with a hole going through it, then $ curl dlvf = vc {0} $ is not a sufficient condition for path independence. In this case, if $dlc$ is a curve going around the hole, then we cannot find a surface inside that domain whose boundary is $dlc$. Without such a surface, we cannot use Stokes theorem to conclude that the cycle around $dlc$ is zero. Read more: how to reverse text in google docs

Last, Wallx.net sent you details about the topic “How To Check If A Vector Field Is Conservative❤️️”.Hope with useful information that the article “How To Check If A Vector Field Is Conservative” It will help readers to be more interested in “How To Check If A Vector Field Is Conservative [ ❤️️❤️️ ]”.

Posts “How To Check If A Vector Field Is Conservative” posted by on 2021-10-27 09:13:12. Thank you for reading the article at wallx.net