Gravitation: Potential | Top Q&A

Attractive potential energy

If gravity moves an object, it acts on that object. However, the amount of work done does not depend on the path that gravity acts on, but on the initial and final positions of the object. This means that gravity is a conservative force. We can sketch a proof of this. Imagine we have a fixed mass M and some other mass m that is moved from A to B by the gravitational force of M. It is clear that any two imaginary lines can be divided into steps. small perpendicular and parallel to the connecting radius M and m. . Since gravity is the central force, perpendicular steps do not contribute to work, since there is no force acting in this direction. Since both paths go from A to B, the sum of their parallel radial segments must be equal. Since the magnitude of the force is equal at equal radial distances, the work must be equal in each case. This path independence allows us to assign a single value to all points a distance r from the source of gravity. We call this value U(r), the gravitational potential energy. As with any potential energy, we need to define some reference point as zero. Therefore, we define U(∞) = 0 and then: Read: why gravitational potential is negative This makes sense as a potential energy. Integral F.dr is the work done to move a particle from infinity to a distance r away from the gravity. According to the work energy theorem, the work done is the change in kinetic energy. We have defined our gravitational potential as the negative of this: when a mass moves towards the gravitational body, it gains kinetic energy (it speeds up). Since all energy is conserved, it must lose an equal amount of potential energy.Read more: why doesn’t my phone vibrate | Top Q&A It’s still integral evaluation. We can do this in any path we choose (since they are all equivalent). We will choose the simplest path: a straight path of radius along the x-axis. In this case, the force is given by and ddx. Hence: We used our definition that U(∞) = 0. The trick is that the gravitational potential energy actually increases with distance. Very close to the attractor M, r is small and U takes on a large negative value. This value increases from a large negative value to a small negative value as the object is moved away from M until the object reaches zero at an infinite distance. Therefore, the gravitational potential energy is always negative.

Attractive field

A useful concept when dealing with forces acting at long distances is the field. Gravitational field lines help us visualize what kind of force would act on a particle at a certain point near another gravitational body. The direction of the line of force indicates the direction of force a mass would endure if placed at a certain point, and the density of the line of force is proportional to the magnitude of the force. Since gravity is a force of gravity, all lines of force point towards mass. shows the distribution of field lines near the two masses. Notice how closely the density of the lines increases with either mass, indicating the increased magnitude of the force at those points.

Attractive potential

Read more: why do I care so much | Top Q&A Sometimes, another concept is defined in relation to gravitational potential energy. We define it here primarily to avoid possible confusion with gravitational potential energy. Gravitational potential energy, Φg, is defined as the potential energy that a unit mass (usually 1 kg) will have at any given point. Mathematically: where M is the mass of the gravitational body. This is sometimes useful because it assigns to each point in space a definite value of gravitational potential energy, regardless of mass.

Gravitational Potential Energy Near Earth

We can see what happens to our expression for near-earth gravitational potential energy. In this case M = I. Consider an object of mass m at a distance r from the center of the earth. Its gravitational potential is: Read more: Why doesn’t yennefer kill cahir Similarly, the gravitational potential at the surface is: The difference in potential energy between these two points is: However, r ± re is simply simply the height h above the earth’s surface and since we are close to the earth (r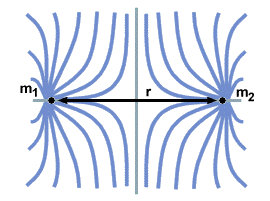re), we can approximate rre = re2. Then we have: since we find in Near-Earth Gravity that g = . This is a familiar result for near-earth gravitational potential energy. Likewise, the gravitational potential near the earth is Φg = gh.

Last, Wallx.net sent you details about the topic “Gravitation: Potential | Top Q&A❤️️”.Hope with useful information that the article “Gravitation: Potential | Top Q&A” It will help readers to be more interested in “Gravitation: Potential | Top Q&A [ ❤️️❤️️ ]”.

Posts “Gravitation: Potential | Top Q&A” posted by on 2021-09-10 11:28:34. Thank you for reading the article at wallx.net