What is the area of the pentagon shown
Video What is the area of a pentagon space of a pentagon is the area enclosed by all 5 sides of the pentagon. A pentagon is a five-sided polygon and a defined two-dimensional geometry. Its identity is derived from the Greek phrases ‘Penta’ meaning ‘5’ and ‘gon’ meaning ‘angles’. In this lesson, we will explore ways to explore the world of pentagons with solved examples and follow-up questions. 1. What is Space of Pentagon? 2. Pentagon Space 3. Find out how to Explore Pentagon Space? 4. Space of Common Pentagon 5. Space of Irregular Pentagon 6. Frequently asked questions about Pentagon Space space of a pentagon is the house coated inside the sides of the pentagon. It can be calculated using different strategies based on a scale that can be determined. It also relies on the type of pentagon. For example, if it is a regular pentagon, the world can be calculated with the help of 1 single formula, however even if it is an irregular pentagon, then we have to cut it into completely different polygons and add their area to get the world. of the pentagon. The area of a pentagon is expressed in square entries like m2, cm2, in2, ft2, etc. Read: What is the area of a pentagon The formula used to search the world of a pentagon varies by type. pentagon. The realm of the pentagonal formula commonly used to search for the world of the everyday pentagon is, Space of the pentagon = 1/2 × p × a Correct here, ‘p’ is the circumference and ‘a’ is the apothem of the pentagon. Observe the next pentagon to see the apothem ‘a’ and the aspect size ‘s’.The realm of a pentagon can be calculated using completely different strategies and formulas based on the possible values provided and added to the pentagon type. Read more: What is 1 divided by infinity | The Realm Q&A of an everyday pentagon can be calculated if only the aspect size ‘s’ is understood. The formula used to find the world of a pentagon daily, (A = frac {1} {4} sqrt {5 (5 + 2sqrt {5})} s^{2}) place ‘s’ is the size of 1 face of the common pentagon.For example: Explore the world of a seven-sided pentagon.Resolution: Lets us use the formula for the world of a daily pentagon = (A = frac {1} {4} sqrt {5 (5 + 2sqrt {5})} s^{2}); position s = 7. After replacing the value of s = 7, we get, (A = frac {1} {4} sqrt {5 (5 + 2sqrt {5})} 7 ^ {2}) = 84.3 sq. The realm of a pentagon can be calculated if aspect and position are given. The commonly used formula for finding the world of any regular polygon using apothem and aspect is, Space of normal polygon = 1/2 × perimeter of polygon × apothem. So, Space of normal pentagon = 1/2 × p × a ; where ‘p’ is the perimeter of the pentagon and ‘a’ is the apothem of the pentagon. Let us perceive this with an example.For example: Explore the world of an everyday pentagon that has an aspect size of eighteen items and an apothem size of 5 items.Resolution: Provided that s = 18 items and a = 5 items, let us discover the perimeter of the pentagon first. Perimeter of pentagon = 5 × frame size = 5 × 18 = 90 items. Now, allow us to substitute these values in the formula Read More: Factor 300 | Q&AS top space of the pentagon, A = 1/2 × p × a; location p = 90, a = 5 ⇒ A = 1/2 × 90 × 5 ⇒ A = 225 square meters of items Then the world of pentagons has an area of 225 square meters of items. pentagon into different smaller polygons. Then the world of those polygons is calculated and added together to get the world of the pentagon. Let us perceive this with an example.For example: Explore the world of regular pentagon ABCDE whose sides are AB = 5 cm, BC = 4 cm, CD = 8 cm, DE = 4 cm, EA = 5 cm.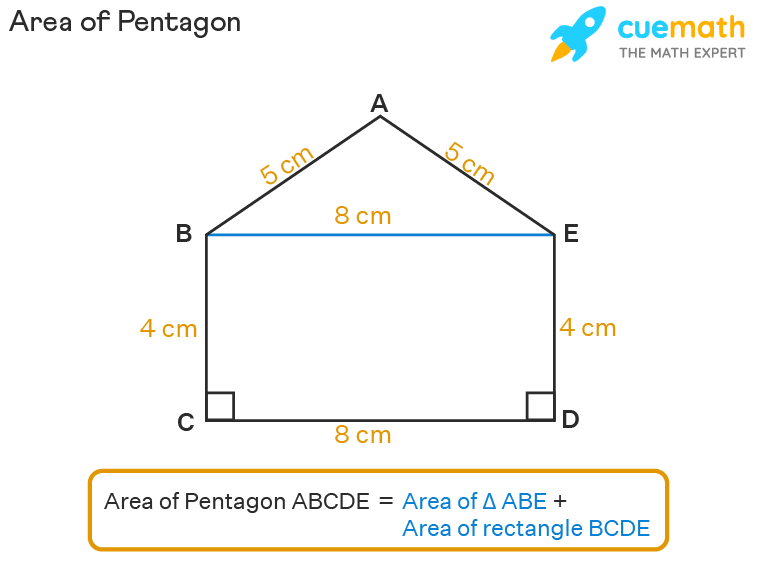
- Step 1: First, we will cut the pentagon into triangle ABE and rectangle BCDE.
- Step 2: Then we will explore the world of triangle ABE and the world of rectangle BCDE. The realm of triangle ABE can be calculated using Heron’s formula since we all know the three sides of the triangle. AB = 5 cm, BE = 8 cm, AE = 5 cm. So the space of triangle ABE =[s(s-a)(s-b)(s-c)]place s = Perimeter / 2 = (a + b + c) / 2. Now, s = (5 + 8 + 5) / 2 = 18/2 = 9. After replacing the values in the formula , we get, Space of ABE =[9(9-5)(9-8)(9-5)] = √ (9 × 4 × 1 × 4) = √144 = 12 cm2.
- Step 3: Area of the rectangle = Size × Width. Right here, Dimensions (CD) = 8 cm, Width (BC) = 4 cm. So rectangular space BCDE = 8 × 4 = 32 cm2.
- Step 4: Add the areas of the triangle and rectangle. Then space of pentagon ABCDE = Space of triangle ABE + Space of rectangle BCDE = 12 + 32 = 44 cm2.
☛ Related ArticlesRead more: What is a percent of 0.5
- Perimeter of the Pentagon
- Space of Sq.
- The space of the circle
- Floor space
- The space of an equilateral triangle
- The space of a parallelogram
- Space of the rectangle
- Space of rhombus
- Space of trapezoid
Last, Wallx.net sent you details about the topic “What is the area of the pentagon shown❤️️”.Hope with useful information that the article “What is the area of the pentagon shown” It will help readers to be more interested in “What is the area of the pentagon shown [ ❤️️❤️️ ]”.
Posts “What is the area of the pentagon shown” posted by on 2022-04-16 16:04:39. Thank you for reading the article at wallx.net

