Sum of Exterior Angles Formula
Video What is the Exterior Angle of a Regular HexagonTotal Exterior Angle Formula Before knowing the formula for the sum of exterior angles, let’s first recall what exterior angles are. The exterior angle of a polygon is the angle between a side face and its adjacent extended edge. This can be clearly understood by observing the outer corners in the triangle below. The sum of exterior angles formula shows that the sum of all exterior angles in any polygon is 360°.Read: what is the outside angle of a regular hexagon
What is the Sum of the Exterior Angle Formula?
From the above triangle, the exterior angles Y and R form a linear pair. (Y + R = 180°). And this gives us, Y = 180° – R. The sum of all three exterior angles of the triangle: Y + R + Y + R + Y + R = 180° + 180° + 180° 3Y + 3R = 540° Sum of the interior angles of a triangle: R + R + R = 180° 3R = 180°. Calculate this in the equation above: 3Y + 180° = 540° 3Y = 540° – 180° 3Y = 360° Hence Sum of Exterior Angles = 360° Thus, sum of all exterior angles of a triangle is 360°. In the same way, we can prove that the sum of all exterior angles of any polygon is 360°. Therefore, the sum of the exterior angles can be calculated by the following formula: Sum of the exterior angles of any polygon = 360° Each exterior angle of a polygon has n faces = 360°/n. More on the formula for the sum of exterior angles.
Solved Examples of Sum of Exterior Angle Formula
Read more: What happened to catherine rose youngExample 1: Find the measure of each circumscribed angle of a regular hexagon.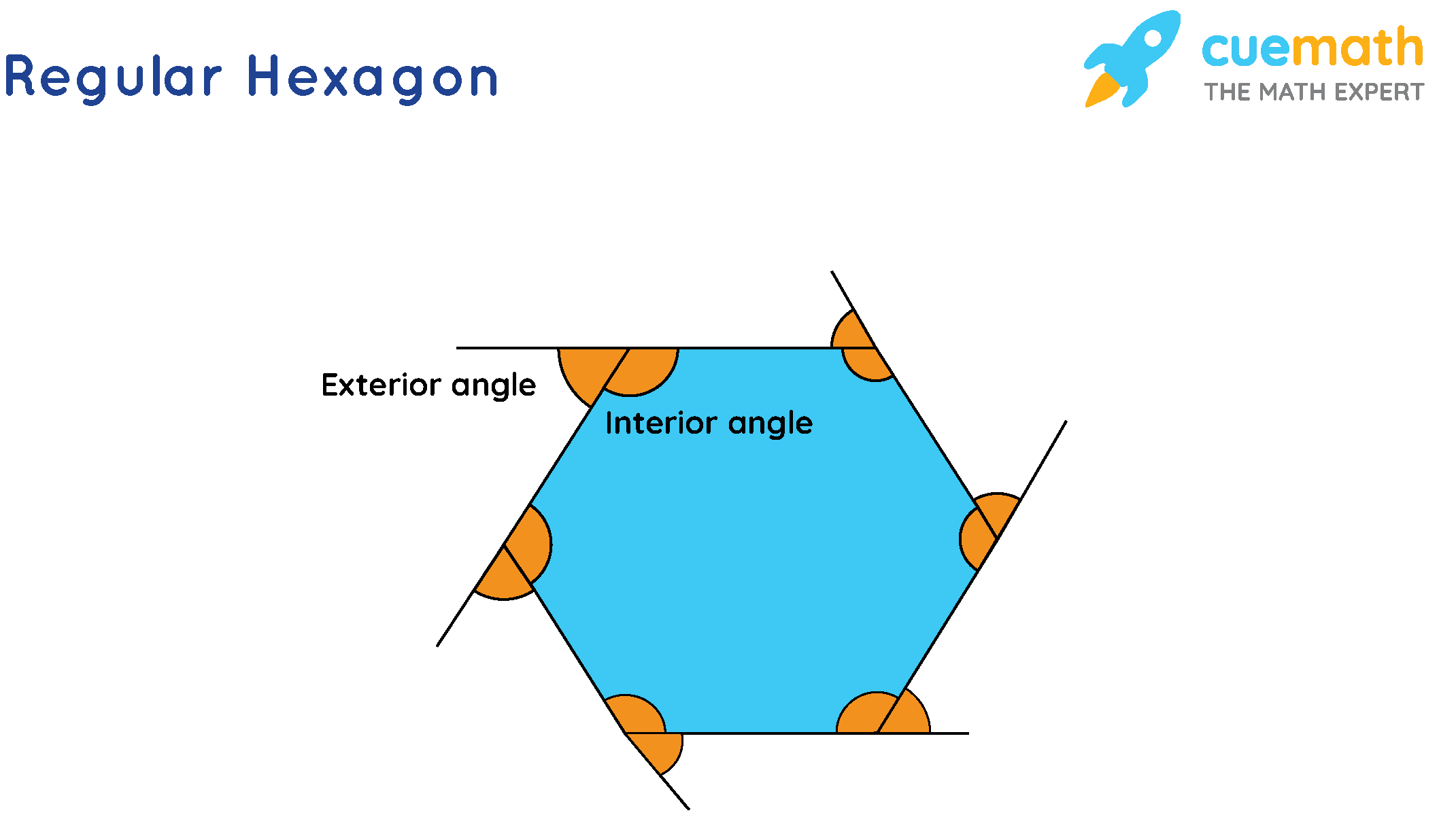
Read more: Introduction to Chemistry | Top Q&ASolution:To find: Measure of each exterior angle of a regular hexagon We know that the number of sides of a hexagon is, n = 6. According to the formula for the sum of exterior angles, Each circumscribed angle of a polyhedron. equilateral triangle with n sides = 360° / n Replace n = 6 here: Each exterior angle of the hexagon = 360° / 6 = 60°Answer: Each exterior angle of a regular hexagon = 60°.Example 2: Use the formula for the sum of exterior angles to prove that each of its corresponding interior and exterior angles in a polygon is additive. Read more: Introduction to Chemistry | Top Q&ASolution:To prove: The sum of an interior angle and its corresponding exterior angle is 180° Let’s consider a polygon with n sides. According to the sum of exterior angles formula, Sum of exterior angles of any polygon = 360° Equal to sum of interior angles formula, Sum of interior angles of any polygon = 180 (n – 2)° Equal by adding the above two equations, we get the sum of n interior angles and the sum of n exterior angles: 360° + 180 (n – 2)° = 360° + 180n – 360° = 180n So the sum of an interior angle and an angle Its corresponding outside is: 180n/n = 180°Answer: Its corresponding interior and exterior angles in any polygon are complementary. Read more: What kind of dog is a woman
Last, Wallx.net sent you details about the topic “Sum of Exterior Angles Formula❤️️”.Hope with useful information that the article “Sum of Exterior Angles Formula” It will help readers to be more interested in “Sum of Exterior Angles Formula [ ❤️️❤️️ ]”.
Posts “Sum of Exterior Angles Formula” posted by on 2021-08-16 07:21:25. Thank you for reading the article at wallx.net
