Square Root of 68 | Top Q&A
Square Root of 68 The square root of 68 is a number that when multiplied by itself gives the product 68. In this lesson, we will calculate the square root of 68 using the long division method along with finding the answer. for the following questions:
- Are all even numbers a perfect square?
- Is the square root of 68 irrational?
Let us find the square root of 68. Read: what is the square root of 68
- Square root of 68: 68 = 8.246
- Square of 68: 682 = 4624
1. What is the square root of 68? 2. Is the square root of 68 Reasonable or Unreasonable? 3. How to find the square root of 68? 4. Think Out of the Box! 5. Frequently Asked Questions about Square Root of 68 6. Important Notes about Square Root of 68 7. Challenge Questions Square root is just an inverse of squares. In the figure below, 2 is the square root of 4, but 4 is a perfect square. Does that mean that numbers that are not perfect squares can’t have square roots? Read more: Focus: The ultimate guide to improving focus and concentrationNon-squared numbers can have square roots, but they won’t be integers. The square root of 68 is represented as √68. The square root of 68 is a number that when multiplied by itself gives us 68. In ancient times, the Greeks figured out a number that cannot be written in the form p / q, where p, q are integers and q ≠ 0 A number that cannot be expressed as a ratio of two integers that are irrational. The decimal form of an irrational number is non-terminating (i.e. it never ends) and non-repeating (i.e. the decimal part of the number never repeats a pattern). Now let’s look at the square root of 68. √68 = 8.24621125124. Do you think the decimal part stops after 8.24621125124? No, it’s never ending and you can’t find a pattern in the decimal part. Therefore, the square root of 68 is an irrational number, we can find the square root of 68 by various methods. 1. Repeated subtraction 2. Prime number calculation 3. Estimation and approximation 4. Long division
Square root of 68 prime factors
Read more: what is the prime factor of 31 | Top Q & ALet try to find the square root of 68 using prime factors. Prime factor of 68 = 2 × 2 × 17 Thus, √68 = √ (2 × 2 × 17) = 2√17 2√17 is in its lowest form and could not be simpler. Thus, we have represented the square root of 68 in root form. Can you try and represent the square root of 26 in a similar way?
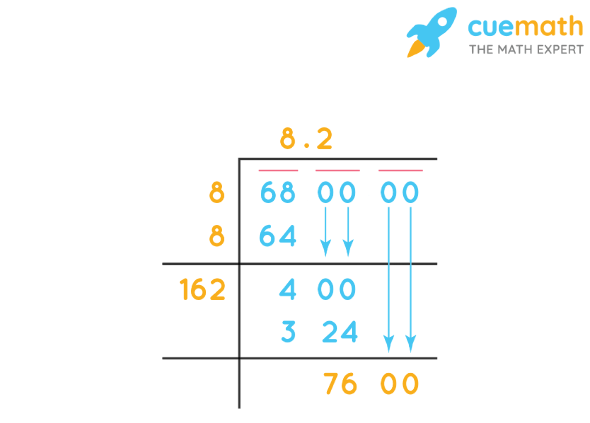
Square root of 68 by length division
The value of the square root of 68 by the long division method involves the following steps.
- Step 1: Find the largest number whose square is less than or equal to 68. Take this as the divisor and quotient (in this case, 8). Divide and write the remainder.
- Step 2: In the quotient, place a decimal point after 8. Bring two zeros to the right of the remainder. Thus, the new dividend is 400.
- Step 3: Double the divisor. Now part of the divisor is 16. Think of a number that has a product very close to 400 and less than or equal to 400. 2 will be the next quotient. Now we get our new divisor of 162, which is 162 × 2 = 324. Do the division and get the remainder.
- Step 4: Repeat this process to three decimal places.
- Square root of 28
- Square root of 34
- Square root of 5
- Square root of 85
- Square root of 8
- Can you think of a perfect squared number after 68?
- Since (√ (-68) 2) = 68, can we say that √ (-68) is also a square root of 68?
- What is the value of the square root of 682?
- Simplify ((√68) )
- Determine the square root of 268.
- The square root of 68 in root form is expressed as 68
- In exponentiation, the square root of 68 is expressed as 68
- The real roots of √68 are ±8.24.
Last, Wallx.net sent you details about the topic “Square Root of 68 | Top Q&A❤️️”.Hope with useful information that the article “Square Root of 68 | Top Q&A” It will help readers to be more interested in “Square Root of 68 | Top Q&A [ ❤️️❤️️ ]”.
Posts “Square Root of 68 | Top Q&A” posted by on 2021-08-14 22:54:03. Thank you for reading the article at wallx.net

