Count Vs. Continuous Variables: Differences Under The Hood
One of the most important concepts in data analysis is that the analysis needs to fit the scale of the variable. The focus of decisions on these scales tends to be on the levels of measurement: nominal, ordinal, interval, ratio Read: what is count data These metrics tell you about the amount of information in the variable. But there are other ways of distinguishing scales that are also important and often overlooked, for example, scale-level variables can be of two types: continuous and discrete. Continuous variables can take any value on a line of numbers, while discrete variables can only take integers. This is important in statistics because we measure different probabilities for discrete and continuous distributions. through a probability distribution. At its simplest, this is a list of all the values in the set and the probability of each occurring, but the probabilities of many discrete random variables following patterns can be described by a mathematical function . This function is called the probability mass function (pmf). As you can imagine, there are many discrete probability distributions. Some of you may have heard of Bernoulli, binomial, supergiant, discrete analogy, and Poisson. There are clear criteria that determine which probability distribution is appropriate for a particular discrete random variable. Quantitative data is a prime example. The counter variable is discrete because it consists of non-negative integers. Even so, there is no one particular probability distribution that fits all count data sets.
Poisson distribution
Read more: What to eat after root canal Poisson distribution is generally consistent with counting data. It is appropriate when the mean of the variable is equal to its variance. So how do you determine that? Run a summary of the variable in your statistics package and compare the mean with the variance. If standard deviation is listed instead of variance, just square the standard deviation. If they’re roughly equal, that’s a good sign. You can also run qqplot of your data against a Poisson distribution. Although we usually use them for normal distributions, you can do it with any of several distributions. However, many counters do not perform these tests. Each has 5,000 observations. The mean of the Poisson data is 2, the variance is 1.99, and the range is 0 to 8. The mean of the negative binomial data is 2, the variance is 4.16, and the range is 0. to 15. the distribution contains an additional parameter that allows the variance to be larger than the mean. If you try to fit that data set with mean and variance with a Poisson distribution, that data set will be considered over-dispersed – not a good fit.Note that there is a probability for each non-negative value on the x-axis, starting with 0. Poisson or a negative binomial random number generator will only produce non-negative integers.
Normal distribution
If the mean of a Poisson or negative binomial variable is high enough, it will be symmetric and bell-shaped. It should look like a normal distribution, except for one key difference – the normal variables are truly continuous, not discrete. They can take on any possible value. Read more: What is a house hippopotamus The result is an infinite number of values (2,30546 is a different value than 2.30547). It makes no sense to compute the probability that X is any exact value in a continuous variable. The probability that the value is a small decimal, a value close to 0. Instead, for continuous variables, the probability that the value falls within a range is calculated. For example, there is a 95% probability that a value from a normal distribution will be within 1.96 standard deviations of the mean of that distribution. and the variance is 2. The range of the data is -2.512433 to 7.461702. Included next to its graph is a graph of the Poisson variable with mean and variance of 2.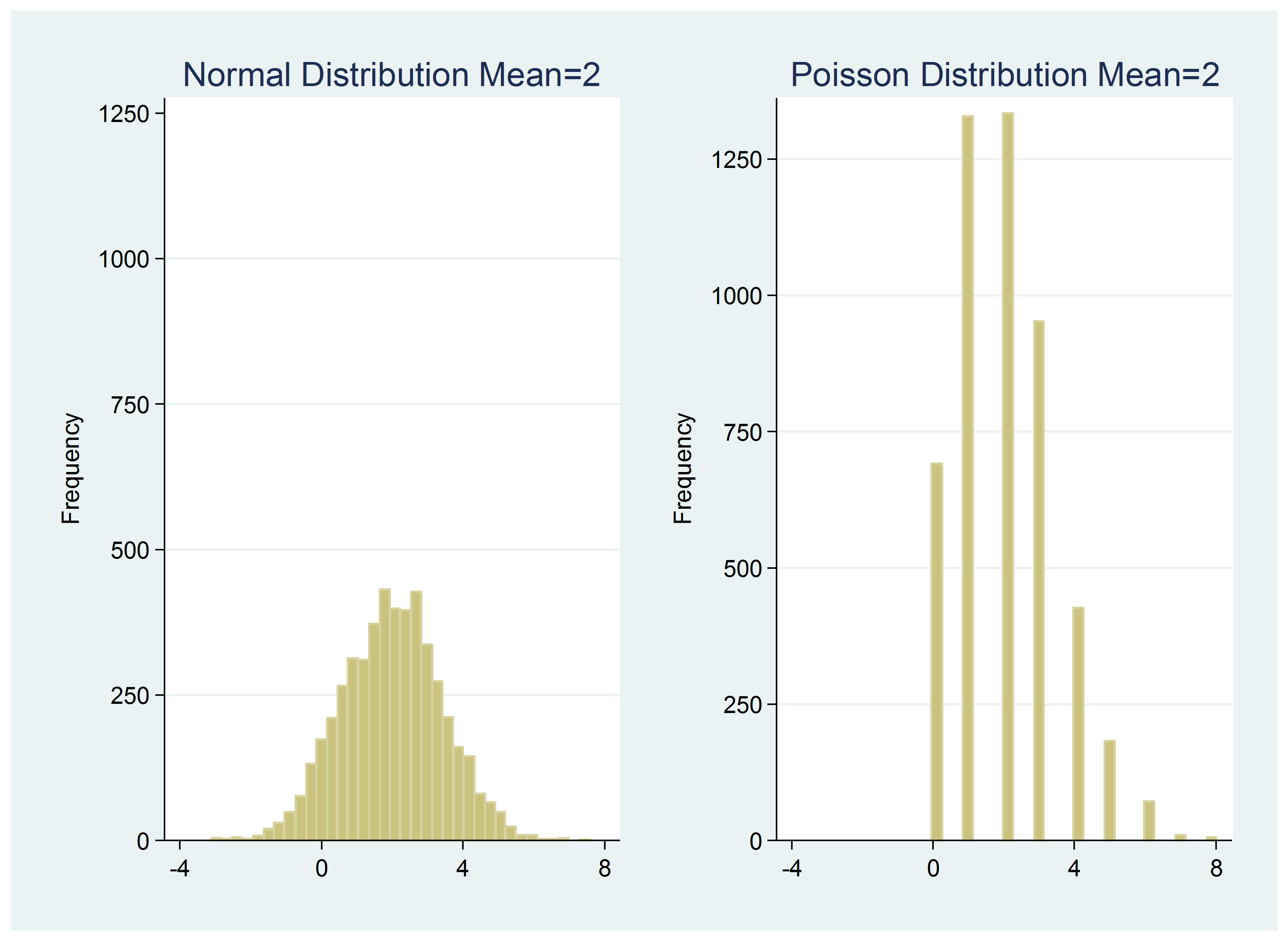
Note the following: Ranges vary greatly (values less than 0 for continuous variables). There is a large difference in the number of unique observations (4,999 for the continuous set and 9 for the discrete Poisson set). check your result variable to determine if it is discrete or continuous. If it is discrete, find the probability distribution function that best fits its structure. Jeff Meyer is a statistical consultant with The Analysis Factor, a statistical advisor to members of Statistical Speaking, and a consultant. workshop guide. Read more about Jeff here. Read more: What is the best alternative to safe refrigerated food
Last, Wallx.net sent you details about the topic “Count Vs. Continuous Variables: Differences Under The Hood❤️️”.Hope with useful information that the article “Count Vs. Continuous Variables: Differences Under The Hood” It will help readers to be more interested in “Count Vs. Continuous Variables: Differences Under The Hood [ ❤️️❤️️ ]”.
Posts “Count Vs. Continuous Variables: Differences Under The Hood” posted by on 2021-09-11 02:53:04. Thank you for reading the article at wallx.net
