what is the prime factorization of 168

Factories of 168 The factors of 168 are numbers that can be evenly divisible by 168. 168 is a three-digit even number, and sure enough, it has many factors, most of which are even. There are 16 factors in the total of 168. Of course, since three digits add to a multiple of 3, 168 is also divisible by 3. In this lesson, we’ll be factoring 168, prime and prime factors. its along with some solved examples for your better understanding.

• Elements of 168: 1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 28, 42, 56, 84 and 168.
• Negative factors of 168: -1, -2, -3, -4, -6, -7, -8, -12, -14, -21, -24, -28, -42, -56, -84 and -168.
• Prime number of 168: 168 = 23 × 3 × 7

1. What are the factors of 168? 2. How to calculate the factors of 168? 3. Factor 168 in primes 4. Challenge question 5. Factor 168 in pairs 6. Important notes 7. Factor 168 FAQ

What are the factors of 168?

The factor of 168 is divisible and has a remainder of 0. When you multiply any two natural numbers and get 168, you can say that both numbers will be factors of 168. For example, you can get 168 as an answer with the following numbers: Read: what is the prime factor of 168

• 1 × 168 = 168
• 2 × 84 = 168
• 3 × 56 = 168
• 4 × 42 = 168
• 6 × 28 = 168
• 7 × 24 = 168
• 8 × 21 = 168
• 2 × 14 = 168

This can be continued until you reach 168 × 1 = 168. Thus, in general, we can say that The factors of 168 are all integers that divide 168 without leaving any remainder.

How to calculate the factors of 168?

Let’s start calculating the factors of 168, starting with the smallest natural number, i.e. 1. Divide 168 by this number. Is the remainder 0? Right! So we will get:

• 168÷ 1 = 168
• 168 × 1 = 168

The next natural number is 2. Now, divide 168 by 2.

• 168 2 = 84
• 84 × 2 = 168

Proceeding in the same way, we get:

• 1 × 168 = 168
• 2 × 84 = 168
• 3 × 56 = 168
• 4 × 42 = 168
• 6 × 28 = 168
• 7 × 24 = 168
• 8 × 21 = 168
• 12 × 14 = 168

Prime factorization means expressing a composite number as its product prime factor.

Basic figures by department

• Step 1: To get the prime factor of 168, we divide it by its smallest prime factor of 2 i.e. 168 ÷ 2 = 84
• Step 2: Now, 84 is divided by its smallest prime factor and the quotient is obtained.
• Step 3: This process is repeated until we get a quotient of 1.

Elemental factors by factor tree

We can do the same process using factor tree as shown in the diagram below:

Basic Database by Upside-Down Division

The prime factor of 168 is shown below:Let us show 168 about the product of key elements like 2 × 2 × 2 × 3 × 7. Q: Now that we’ve done the prime factorization of our numbers, we can multiply those numbers and get other factors. Can you try and find out if all the elements are covered or not? ONE: As you may have guessed, for prime numbers, there are no other factors. Explore the elements using interactive illustrations and examples:

• Factories of 36 – The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.
• Factors of 24 – The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
• Factors of 15 – The factors of 15 are 1, 3, 5 and 15.
• The coefficients of 45 – The coefficients of 45 are 1, 3, 5, 9, 15 and 45.
• Factories of 72 – The factors of 72 are 1, 2, 3, 4, 6, 8, 9 12, 18, 24, 36 and 72.
• Factories of 48 – The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.

Read more: How to remove Ecp.yusercontent.com from computer | Top Q&AChallenge question:

• Identify several other numbers with only one a factor pair.
• Can multiples of 168 also be a factor of 168?

Elements of 168 in pairs

Pairs that give 168 when multiplied are called factors of 168. Here are the factors of 168 in the pairs:Product model 168 Pair element1 × 168 = 168 (1,168) 2 × 84 = 168 (2, 84) 3 × 56 = 168 (3.56) 4 × 42 = 168 (4, 42) 6 × 28 = 168 (6, 28) 7 × 24 = 168 (7, 24) Read more: eyes can’t see | Top Q & A8 × 21 = 168 (8, 21) 12 × 14 = 168 (12, 14) 14 × 12 = 168 (14,12) 21 × 8 = 168 (21, 8) You can observe the table above , after 12 × 14, the elements start repeating, except that they appear in a different order. So it is enough just to find the factors until (12, 14) The pairs of factors of 168 are: (1, 168), (2, 84), (3, 56), (4, 42), (6, 28), (7, 24), (8, 21) and (12, 14).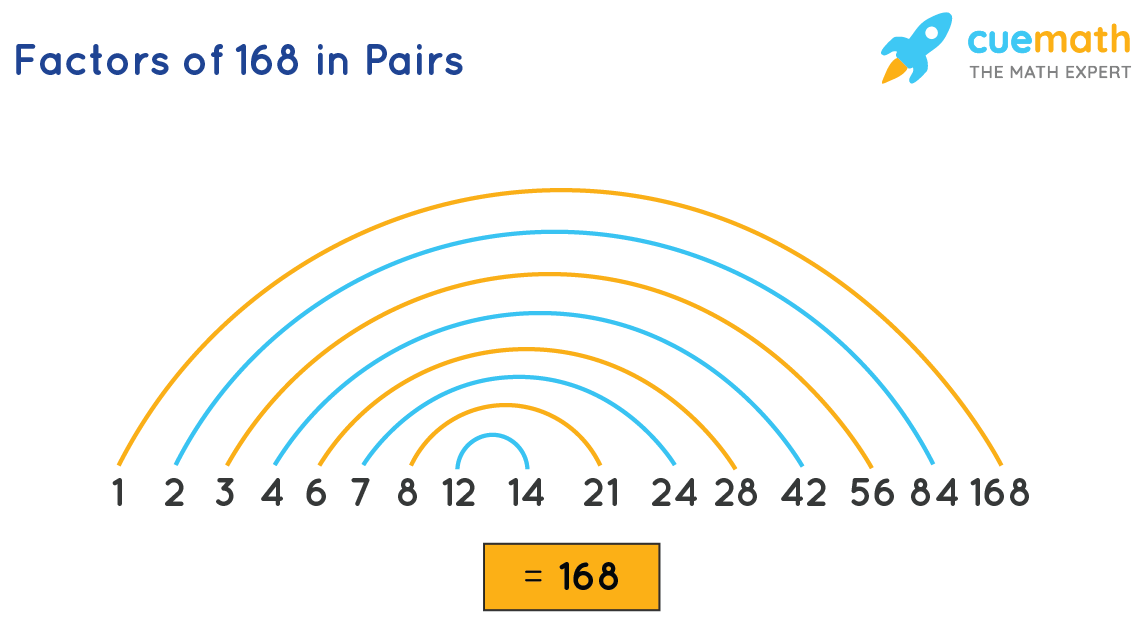Let’s take a look at negative pair elements out of 168.Read more: What color do purple and orange make

• If we consider negative integers, both numbers in the factor pair will be negative.
• There can also be negative pairwise factors because the product of two negative numbers gives a positive number.
• Therefore, we can have pairs of factors 168 as (-1, -168), (-2, -84), (-3, -56), (-4, -42), (-6, -28), (-7, -24), (- 8, -21) and (-12, -14).

• The smallest factor of 168 is 1 and the largest factor of 168 will be the number itself, which is 168.
• Fractions and decimals cannot be factors. Only integers (positive or negative) can be factors.
• The factors of 168 are 1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 28, 42, 56, 84, and 168.

Last, Wallx.net sent you details about the topic “what is the prime factorization of 168❤️️”.Hope with useful information that the article “what is the prime factorization of 168” It will help readers to be more interested in “what is the prime factorization of 168 [ ❤️️❤️️ ]”.

Posts “what is the prime factorization of 168” posted by on 2021-09-13 21:16:39. Thank you for reading the article at wallx.net