Identity Function | Top Q&A
The identification function is a function that returns the same value, used as its argument. It is also known as identity relationship or identification map or change identity. If f is a function, then the identity relation for the argument x is expressed as f(x) = x, for all values of x. In terms of relations and functions, the function f: P → P is determined by b = f (a) = a for each a ϵ P, where P is the set of real numbers. Both the domain and extent of the function here are P and the plotted graph will show a line passing through the origin.
Identification function definition
Contents
Let R be the set of real numbers. Therefore, a function with a real value f: R → R in terms of y = f(a) = a for all a ∈ R, is called an identity function. Here the domain and extent (co-domain) of the function f is R. Therefore, each element of the set R has an image on itself. The graph is a straight line and it passes through the origin. The application of this function can be seen in the identity matrix. Read: what is the identity function Physically, it can be expressed as; Where a is an element of the set R. For example, f(2) = 2 is an identity function. Theoretically, when a function is described as a particular type of binary relation, the identity function is given by the identity or diagonal relation of A, where A is a set.Also, read:
Graph of identification function
If we plot the identity function, it will appear to be a straight line. Let’s draw a graph for the function f(x) = x, by setting different values of x. Therefore, let’s draw a histogram based on these values.So, from the graph above, it is clear that the function is similar to a line in the xy plane.Read more: इंडिगो पाउडर क्या है, इससे बाल काले करने का तरीका | Let us tackle some examples based on this concept.
Example of identification function
H.1: Prove that f(2x) = 2x is a similar function.Solution: Given, f (2x) = 2x Put the values of x into the given function, if x = 1 then f (2 (1)) = 2 (1) ⇒ f (2) = 2If x = 2 , then; f (2 (2)) = 2 (2) ⇒ f (4) = 4If x = 3 then; f (2 (3)) = 2 (3) ⇒ f (6) = 6If x = 0 , then; Read more: Pc Gaming Info and Reviews | Top Q & Af (2 (0)) = 2 (0) ⇒ f (0) = 0 Let us try with some negative values of x. If x = -1 then; f (2 (-1)) = 2 (-1 ) ⇒ f (-2) = -2If x = -2 then f (2 (-2)) = 2 (-2) ⇒ f (-4) = – 4If x = -3 then f(2(-3)) = 2(-3) f(-6) = -6 Let’s draw a table for all values of x Let’s plot the values this.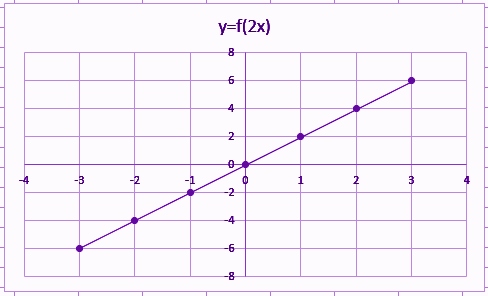
Attribute of identification function
- It is a linear operator in the application case of vector spaces.
- For positive integers, it is a multiplication function.
- For the m-dimensional vector space, it is represented as the identity matrix Im.
- In topological space, this function is always continuous.
Last, Wallx.net sent you details about the topic “Identity Function | Top Q&A❤️️”.Hope with useful information that the article “Identity Function | Top Q&A” It will help readers to be more interested in “Identity Function | Top Q&A [ ❤️️❤️️ ]”.
Posts “Identity Function | Top Q&A” posted by on 2021-08-30 00:17:05. Thank you for reading the article at wallx.net

